作用

gram矩阵是计算每个通道 I 的feature map与每个通道 J 的feature map的内积。

gram matrix的每个值可以说是代表i通道的feature map与j通道的feature map的互相关程度

神经网络风格迁移中的作用
Gram矩阵来表示图像的风格特征。Gram Matrix的特点：注重风格纹理等特征，忽略空间信息。

$C\times H\times W$，C是卷积核的通道数，一般称为有C个卷积核。每一个卷积核输出的HxW代表这张图像的一个 feature map，可以认为是一张特殊的图像——原始彩色图像可以看作RGB三个feature map拼接组合成的特殊feature maps。

• Gram Matrix的计算采用了累加的形式，抛弃了空间信息。一张图片的像素随机打乱之后计算得到的Gram Matrix和原图的Gram Matrix一样。所以可以认为Gram Matrix抛弃了元素之间的空间信息。

• ·Gram Matrix的结果与feature maps的尺度无关，只与通道数有关。无论H、W的大小如何，最后Gram Matrix的形状都是C×C。

• 对于一个CxH×W的feature maps，可以通过调整形状和矩阵乘法快速计算它的Gram Matrix，即先将F调整为Cx（HW）的二维矩阵，然后再计算F.FT，结果就是Gram Matrix。

Gram矩阵

Gram矩阵计算

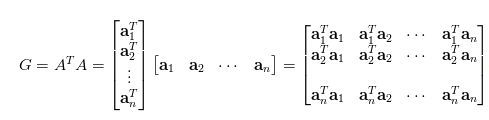
Gram矩阵定义

协方差矩阵

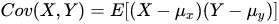
公式简单翻译一下是：如果有XY两个变量，每个时刻的“X值与其均值之差”乘以“V值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值（其实是求“期望”，但就不引申太多新概念了，简单认为就是求均值了）。

Gram矩阵和协方差矩阵

Gram矩阵和协方差矩阵的差别在于，Gram矩阵没有白化，也就是没有减去均值，直接使用两向量做内积。

Gram矩阵和相关系数矩阵的差别在于，Gram矩阵既没有白化，也没有标准化（也就是除以两个向量的标准差）。

这样，Gram所表达的意义和协方差矩阵相差不大，只是显得比较粗糙。两个向量的协方差表示两向量之间的相似程度，协方差越大越相似。对角线的元素的值越大，表示其所代表的向量或者说特征越重要。

Gram矩阵意义

   格拉姆矩阵可以看做feature之间的偏心协方差矩阵（即`没有减去均值的协方差矩阵`），在feature map中，每个数字都来自于一个特定滤波器在特定位置的卷积，因此每个数字代表一个特征的强度，而Gram计算的实际上是两两特征之间的相关性，哪两个特征是同时出现的，哪两个是此消彼长的等等，同时，Gram的对角线元素，还体现了每个特征在图像中出现的量，因此，`Gram有助于把握整个图像的大体风格`。有了表示风格的Gram Matrix，要度量两个图像风格的差异，只需比较他们Gram Matrix的差异即可。


   总之， 格拉姆矩阵用于度量各个维度自己的特性以及各个维度之间的关系。内积之后得到的多尺度矩阵中，对角线元素提供了不同特征图各自的信息，其余元素提供了不同特征图之间的相关信息。这样一个矩阵，既能体现出有哪些特征，又能体现出不同特征间的紧密程度。

计算实例

$$\begin{gathered} G=[ \\ x{1}^{\prime }\ast x1,x{1}^{\prime }\ast x2,x{1}^{\prime }\ast x3; \\ x{2}^{\prime }\ast x1,x{2}^{\prime }\ast x2,x{2}^{\prime }\ast x3; \\ x{3}^{\prime }\ast x1,x{3}^{\prime }\ast x2,x{3}^{\prime }\ast x3] \end{gathered}$$

$G[0,0]=x_1^{\prime }\ast x_1=3\ast 3+3\ast 3=18$
$G[0,1]=x_2^{\prime }\ast x_1=4\ast 3+3\ast 3=21$

• 参考文献

Gram矩阵_matlab_wangyang20170901的博客-CSDN博客
https://blog.csdn.net/wangyang20170901/article/details/79037867/

如何通俗易懂地解释「协方差」与「相关系数」的概念？ - GRAYLAMB的回答 - 知乎
https://www.zhihu.com/question/20852004/answer/134902061

如何用简单易懂的例子解释格拉姆矩阵/Gram matrix？ - 知乎
https://www.zhihu.com/question/49805962