GBDT 自动化特征工程与 LR 在推荐系统中的应用

GBDT（Gradient Boosting Decision Trees）的核心原理是基于决策树的集成，通过逐步修正每棵树的预测误差，来优化整体模型的预测性能。每一棵树都是根据前一棵树的残差（预测误差）进行训练的，从而在模型训练过程中逐渐减少误差。具体来说，GBDT通过引入新树来减少当前预测值与真实标签之间的差异，这一过程能够使得模型逐步接近真实的拟合函数。每棵树在进行节点分裂时，实际上是对特征

Asuka@

2473人浏览 · 2025-01-26 15:11:23

Asuka@ · 2025-01-26 15:11:23 发布

实验和完整代码

完整代码实现和jupyter运行：https://github.com/Myolive-Lin/RecSys--deep-learning-recommendation-system/tree/main

引言

推荐系统作为一种复杂的机器学习应用，面临着大量的特征选择和组合问题。传统方法通常依赖人工构建特征，或者通过手动优化模型的目标函数来增加特征交叉。然而，这些方法往往需要大量的人工干预和高昂的计算代价，且难以处理高维特征组合。随着模型复杂度的增加，特征交叉的处理成为了一个重要的瓶颈。2014年，Facebook提出了结合 GBDT 和 LR（逻辑回归）模型的方案，为这一问题提供了一种新的解决思路，开创了特征工程模型化的新时代。

1. GBDT+LR 模型结构

GBDT（梯度提升决策树）和LR的组合利用了GBDT强大的特征筛选与自动特征组合能力，再将这些特征传递给LR进行预测。这一结构的关键在于，GBDT与LR的训练过程是独立进行的，因此无需担心梯度回传的问题。具体而言，GBDT通过训练多棵决策树，对输入数据进行特征筛选与自动组合，生成新的特征向量，最后将这些特征向量作为输入传递给LR模型，用于预估CTR（点击率）等目标值。

2. GBDT模型简介

GBDT（Gradient Boosting Decision Trees）的核心原理是基于决策树的集成，通过逐步修正每棵树的预测误差，来优化整体模型的预测性能。每一棵树都是根据前一棵树的残差（预测误差）进行训练的，从而在模型训练过程中逐渐减少误差。具体来说，GBDT通过引入新树来减少当前预测值与真实标签之间的差异，这一过程能够使得模型逐步接近真实的拟合函数。每棵树在进行节点分裂时，实际上是对特征进行选择和组合，从而提升了模型对复杂数据的处理能力。

假设当前森林已有三棵树，当前的预测值为：

$D (X) = d t ree 1 (x) + d t ree 2 (x) + d t ree 3 (x)$

新树的目标是最小化当前模型的预测值与真实值之间的差距。因此，第四棵树将根据当前预测值与真实标签之间的残差来进行训练：

$r (x) = F (X) - D (X)$

随着树的数量不断增加，GBDT能够逐步逼近真实的拟合函数，从而展现出其强大的预测能力

3. GBDT进行特征转换

例子：

假设我们有一棵GBDT模型，其中包含三棵树，每棵树有5个叶子节点。当输入一个样本时，样本会经过每棵树，并且每棵树会根据样本的特征将其分配到一个特定的叶子节点。每个叶子节点的编号将作为一个特征值。

第一棵树：输入样本进入第2个叶子节点，因此该树的特征向量为 [0, 1, 0, 0, 0]。
第二棵树：输入样本进入第4个叶子节点，因此该树的特征向量为 [0, 0, 0, 1, 0]。
第三棵树：输入样本进入第1个叶子节点，因此该树的特征向量为 [1, 0, 0, 0, 0]。

最终，我们将这三棵树的特征向量拼接起来，形成一个新的特征向量：

$[0, 1, 0, 0, 0] + [0, 0, 0, 1, 0] + [1, 0, 0, 0, 0]$

拼接后的最终特征向量为：

$[0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0]$

这一新的特征向量将作为逻辑回归（LR）模型的输入，LR模型将基于这些特征进一步进行分类或回归预测。
通过这一方式，GBDT不仅实现了自动化的特征选择，还为每个样本生成了高效的特征表示，这些特征将用于后续的预测任务，而不需要手动进行复杂的特征组合和筛选。这种特征转换的能力使得GBDT在许多机器学习任务中具有强大的表现力和适应性。

4 GBDT的数学公式

GBDT的训练过程可以通过以下步骤来理解：

初始化模型：首先，用常数值初始化模型。对于回归问题，通常选择目标变量的均值作为初始预测值：
$F_0(x) = \arg\min_\gamma \sum_{i=1}^n L(y_i, \gamma)$
其中， $L$ 是损失函数， $y_i$ 是样本的真实值， $F_0(x)$ 是初始预测值，通常选择为所有样本的均值。
计算残差：根据当前模型 $F_m(x)$ 计算每个样本的残差 $r_i^{(m)}$ ，即真实值与预测值之间的差异：

$r_i^{(m)} = -\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}$

其中， $L(y_i, F(x_i))$ 是损失函数， $r_i^{(m)}$ 表示在第 $m$ 轮迭代中，样本 $i$ 的梯度（残差）。

如果选择MSE作为损失函数，那么残差就为 $y_i - F(x_i))$ ,比如对于一个样本,x = 1, y = 2 , $模型预测值F_0$ = 4, 那么 $r_1$ = -(2 - 4) = 2
拟合残差：用一个新的决策树 $h_m(x)$ 来拟合这些残差。目标是通过决策树模型 $h_m(x)$ 来最小化残差的平方误差：
$h_m(x) = \arg\min_{h} \sum_{i=1}^n \left( r_i^{(m)} - h(x_i) \right)^2$
这棵树的输出是对当前残差的最优拟合。
更新模型：根据树 $h_m(x)$ 的输出结果更新模型。更新方式为：
$F_{m+1}(x) = F_m(x) + \nu h_m(x)$
其中， $\nu$ 是学习率，用于控制每棵树对最终模型的贡献大小。
重复训练：重复步骤2到步骤4，直到达到预定的树的数量或损失函数收敛为止。

值得注意有两个地方

误差不一定最优：直接计算预测值与真实值之间的差异（如 $y_i - F(x_i)$ ）仅仅给出一种误差的度量，但这个误差并不能告诉我们如何改进当前模型。梯度给出了如何调整模型参数以更有效地减少误差。
梯度反映了误差变化的方向：通过计算梯度，我们可以了解在当前模型下，如何改变模型预测值 $F (x)$ ，使得损失函数 $L$ 更小。也就是说，梯度下降法利用了梯度信息来找到损失函数下降最快的路径，从而提高模型的预测能力。

损失函数

GBDT的核心思想是通过梯度下降来最小化损失函数。在回归问题中，常用的损失函数是均方误差（MSE）：

$\frac{1}{2}(y - F(x))^2$

而在分类问题中，常用的损失函数是对数损失（log loss）：

$-\left( y \log(F(x)) + (1 - y) \log(1 - F(x)) \right)$

梯度下降的关键在于计算损失函数关于模型预测值的梯度，用来指导每棵树的训练方向。

模型优化与正则化

为了防止过拟合，GBDT模型通常引入正则化项。对于每棵树 $h_m(x)$ ，可以添加正则化项以控制树的复杂度，常见的正则化方法包括限制树的最大深度、叶节点的最小样本数等。

结果更新与最终模型

最终模型是所有树的加权组合，模型的预测结果为：

$F_0(x) + \sum_{m=1}^M \nu h_m(x)$

其中， $M$ 为树的数量， $\nu$ 为学习率，控制每棵树对最终结果的贡献。

另外逻辑回归的原理在之前的博客已经进行讲解，感兴趣的可以去看看

5. 实战和代码实现

code

(注意完整代码可在上面的Github链接中获取)

# 转换成叶子结点特征
def transform_to_leaf_features(gbdt, X):
    """
    gbdt: GBDT model
    X: input data
    return: leaf features
    """

    #获取样本落入每一颗树的叶子结点的索引
    leaf_indices  = gbdt.apply(X) #X_leaves : array-like of shape (n_samples, n_estimators, n_classes)
    leaf_indices = leaf_indices.reshape(X.shape[0],-1)

    leaf_indices = leaf_indices.astype(int)

    #对树叶子结点进行one-hot编码
    #可以用sklearn内置的OneHotEncoder().fit_transform(res).toarray(),但这里为了学习,还是采用手撕方式
    n_estimators = leaf_indices.shape[1]
    n_leaves = int(np.max(leaf_indices)) + 1 #每一个ont-encode的列数
    transformed_matrix = np.zeros((X.shape[0], n_estimators * n_leaves),dtype= int)

    for i in range(n_estimators):
        for j in range(X.shape[0]):
            transformed_matrix[j, i * n_leaves + leaf_indices[j,i] ] = 1

    return transformed_matrix

#数据预处理
X,y = make_classification(
    n_samples = 1000,
    n_features = 20,
    n_informative = 15, #指定其中有多少个特征是“信息性”的（即对分类目标有帮助的）
    n_redundant = 5, #指定有多少个特征是“冗余”的。冗余特征是通过将信息性特征进行线性组合生成的
    random_state = 42 
)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 训练GBDT模型
gbdt = GradientBoostingClassifier(
    n_estimators = 100, # 使用100个决策树
    max_depth = 4, # 树的最大深度为4
    learning_rate = 0.1,
    random_state = 42
)

gbdt.fit(X_train, y_train)

# 利用GBDT生成新的特征
X_train_transformed = transform_to_leaf_features(gbdt, X_train)
X_test_transformed = transform_to_leaf_features(gbdt, X_test)

# 训练LR模型
lr = LogisticRegression(max_iter = 1000, random_state = 42)
lr.fit(X_train_transformed, y_train)

实验结果

得到评价指标如下

	Precision	Recall	F1-Score	Support
	0.94	0.90	0.92	160
	0.89	0.94	0.91	140
Accuracy			0.92	300
Macro avg	0.92	0.92	0.92	300
Weighted avg	0.92	0.92	0.92	300

混淆矩阵和roc_auc图

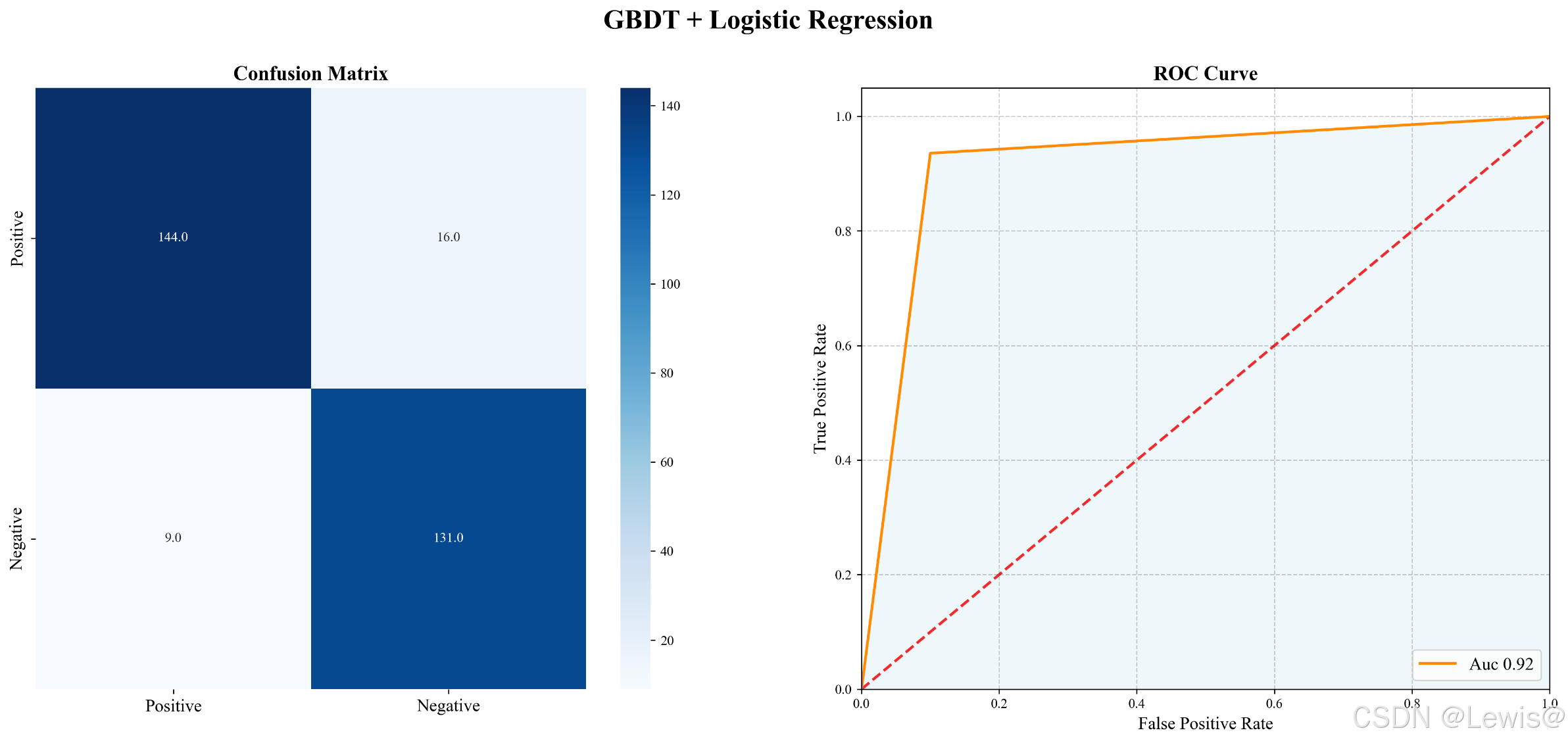
在这里插入图片描述

综合来看 GBDT + LR的模型还不错，但GBDT容易过拟合，以及GBDT的特征转换方式实际上丢失了大量特征信息的数据信息并且因为使用One-hot需要存储更多额外数据，因此不能简单的数据说GBDT的特征交叉能力强，效果比其他模型好，在模型的选择和调试上，永远都是多种因素综合作用的结果

6. GBDT+LR的优势和局限性

GBDT通过决策树的深度来决定特征交互的复杂度。
当树的深度增加时，通过多个节点的分裂可以获得更高阶的特征组合。这一特性使得GBDT在捕捉特征间的复杂交互关系上具备显著优势，尤其是在处理非线性特征时表现尤为突出。与FM（因子分解机）等模型相比，GBDT能够自然而高效地处理特征交叉。例如，树的深度为4时，每个叶节点代表了一个三阶特征交叉。因此，GBDT具有强大的特征建模能力，能够通过逐层树的分裂有效提升模型的预测精度。
GBDT也存在一定的局限性
尤其在处理小样本数据或特征选择不充分的情况下，容易出现过拟合。此外，由于其特征转换过程依赖于叶子节点的离散表示，可能导致部分细粒度信息的丢失。因此，虽然GBDT在特征交叉方面表现强劲，但其应用场景仍需谨慎考虑

GBDT+LR的组合模型则有效融合了两者的优势，尤其在推荐系统等任务中，提供了更为显著的解决方案，具体表现在以下两个方面：

自动化特征工程：传统特征工程需要依赖人工设计和筛选特征，过程既繁琐又容易遗漏重要特征。而GBDT+LR的组合模型能够通过GBDT自动学习并生成高效的特征组合，从而减少了人工干预。这种自动化特征工程不仅提升了特征选择的效率，也降低了人为因素对模型性能的影响。
端到端训练流程：GBDT和LR的训练过程可以独立进行，且无须过多的人工干预，支持端到端的训练。这一自动化流程不仅减少了模型训练的复杂性，也使得模型在大规模数据处理中的扩展性得到了极大提升。

在推荐系统中，GBDT+LR组合模型能够有效提高特征的表达能力，并在庞大的数据集中筛选出最具价值的特征。这使得该模型在点击率预测（CTR）、用户行为分析、商品推荐等任务中展现出优越的性能，特别是在处理大规模数据时，能够提供高效且精准的预测结果。